(a-b)^2 260931-B 25 bomber
\ a = \sqrt{c^{2} b^{2}} \ Solve for the Length of Side b The length of side b is the square root of the squared hypotenuse minus the square of side a \ b = \sqrt{c^{2} a^{2}} \ Solve for Area A of the Right Triangle The area of a right triangle is side a multiplied by side b divided by 2= a 2 ab ac ba b 2 bc ca cb c 2 Adding like terms, the final formula (worth remembering) is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2acFirst, we can expand the first equation as (a b)2 = 9 a2 2ab b2 = 9 Next, we can expand the second equation as (a −b)2 = 49 a2 −2ab b2 = 49 Then, we can add the left side of each equation and the right side of each equation giving a2 2ab b2 a2 − 2ab b2 = 9 49 a2 a2 2ab −2ab b2 b2 = 58

If A 2 B C B 2 C A C 2 A B Are In Ap Then Prove That A B C Are In Ap Mathematics Topperlearning Com Yzhqah
B 25 bomber
B 25 bomber-Discrete Data Sets Mean, Median and Mode Values Calculate arithmetic mean2 29 if a ib=0 wherei= p −1, then a= b=0 30 if a ib= x iy,wherei= p −1, then a= xand b= y 31 The roots of the quadratic equationax2bxc=0;a6= 0 are −b p b2 −4ac 2a The solution set of the equation is (−b p 2a −b− p 2a where = discriminant = b2 −4ac 32



16 A B 2 9 A B 2 Factorise Brainly In
Free expand & simplify calculator Expand and simplify equations stepbystepSquare Formulas (a b) 2 = a 2 b 2 2ab (a − b) 2 = a 2 b 2 − 2ab a 2 − b 2 = (a − b) (a b) (x a) (x b) = x 2 (a b) x ab (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca (a (−b) (−c)) 2 = a 2 (−b) 2 (−c) 2 2a (−b) 2 (−b) (−c) 2a (−c) (a – b – c) 2 = a 2 b 2 c 2 − 2ab 2bc − 2caHolds only in fields of characteristic 2, which if finite, must have 2^m elements, where m is a positive integer Also holds in the (infinite) field of rational functions over such a field
What does (ab)^2 and (ab)^2 equal?" You are squaring two different binomials When you square a binomial, you multiply it by itself (a b)^2 = (a b)(a b) = a(a) a(b) b(a) b(b) {used foil method} = a^2 ab ab b^2 {multiplied through} = a^2 2ab b^2 {combined like terms}I am currently working on spivak calculus 4th edition One of the problem asks the following Prove that if $0 < a < b$ $ a < \sqrt(ab) < (ab)/2 < b$Show that (AB)^2,(A^2B^2),(AB)^2 is an AP Ask questions, doubts, problems and we will help you menu myCBSEguide Courses CBSE Entrance Exam Competitive Exams ICSE & ISC Teacher Exams UP Board Uttarakhand Board Features Online Test Practice Homework Help Downloads CBSE Videos Courses
$\implies$ $(ab)^2 \,=\, a^2b^22ab$ Simplification The subtraction of two times product of two terms from the sum of the squares of the terms is simplified as the square of difference of the terms2ac2bc3ad3bd Factorization found (2c 3d) • (a b) Trying to factor a multi variable polynomial 11 Split 2ac 2cb 3ad 3bd into two 2termRelated Topics Mathematics Mathematical rules and laws numbers, areas, volumes, exponents, trigonometric functions and more ;



Abc Is An Isosceles Triangle Right Angled At C Prove That Ab 2 2ac 2



Boss Ab 2 2 Way Selector Pedal Sweetwater
Section 23 Key Point In general, detAdetB ̸= det( AB);(a − b) 2 = (a − b)(a − b) = a(a − b) − b(a − b) = a 2 − ab − ba b 2 = a 2 − 2ab b 2 Practice Exercise for Algebra Module on Expansion of (a ± b) 2 Algebra (x±a)(y±b) by FOILComplex Numbers Complex numbers are used in alternating current theory and in mechanical vector analysis;



Dopl3r Com Memes Lmao These Are So True00 A B Ab Ab Ab 2 32 3 5 A3 A B Ab B2 A3 A B Ab


Search Q A B 5e2 Examples Tbm Isch
(ab) 2 = a 2 2ab b 2 (ab)(cd) = ac ad bc bd a 2 b 2 = (ab)(ab) (Difference of squares) a 3 b 3 = (a b)(a 2 ab b 2) (Sum and Difference of CubesSimplify (ab)^2(ab)^2 Simplify each term Tap for more steps Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more stepsBy closure under addition, (ba)(ba)>0 Or, b^2a^2>0 Or, b^2>a^2 Or, a^2


What S The Formula Of A B Quora



Factorisation Using A B 2 A B 2 B2 Identities Teachoo
A review of the difference of squares pattern (ab)(ab)=a^2b^2, as well as other common patterns encountered while multiplying binomials, such as (ab)^2=a^22abb^2 Google Classroom Facebook Twitter(ab)^2 = a^2 2abb^2 this equation 1 (ab)^2 = a^2 2abb^2 this equation 2 (ab)^2 (ab)^2 = equation 1 equation 2 = a^2 2abb^2 (a^2 2abb^2)Simplify the Algebraic expression The square of sum of terms a and b is expanded as an algebraic expression a 2 a b b a b 2 According to commutative property, the product of a and b is equal to the product of b and a So, a b = b a ( a b) 2 = a 2 a b a b b 2



How To Prove Math A 2 B 2 C 2 Ab Ca Math Is Non Negative For All Values Of Math A B Math And Math C Quora



Algebra Sleuth Proof That 1 2 Activity Education Com
Binomial Theorem (ab)1 = a b ( a b) 1 = a b (ab)2 = a2 2abb2 ( a b) 2 = a 2 2 a b b 2 (ab)3 = a3 3a2b 3ab2 b3 ( a b) 3 = a 3 3 a 2 b 3 a b 2 b 3 (ab)4 = a4 4a3b 6a2b2 4ab3 b4 ( a b) 4 = a 4 4 a 3 b 6 a 2 b 2 4 a b 3 b 4Thus the expansion for (a b) 6 is (a b) 6 = 1a 6 6a 5 b 15a 4 b 2 a 3 b 3 15a 2 b 4 6ab 5 1b 6 To find an expansion for (a b) 8, we complete two more rows of Pascal's triangle Thus the expansion of is (a b) 8 = a 8 8a 7 b 28a 6 b 2 56a 5 b 3 70a 4 b 4 56a 3 b 5 28a 2 b 6 8ab 7 b 8 We can generalize ourGeometrical proof of ab whole square formula with procedure to derive expansion of (ab)^2 identity is equal to a²2abb² in algebraic mathematics



Solved Real Numbers A B C Natural Number N 65 A1 B Chegg Com



ब जगण त Identity भ ग 2 How To Use Algebraic Identity A B 2 In Hindi Youtube
Definition The longest side of the triangle is called the "hypotenuse", so the formal definition isSee below mathbf A times mathbf B = mathbf A mathbf B sin alpha \ hat (mathbf n) mathbf A * mathbf B = mathbf A mathbf B cos alpha implies mathbf A timesFor a square b square watch http//youtube/24gWbMSEVVwLearn how a minus b whole square can be explained using geometrical drawingsFor more such videos v
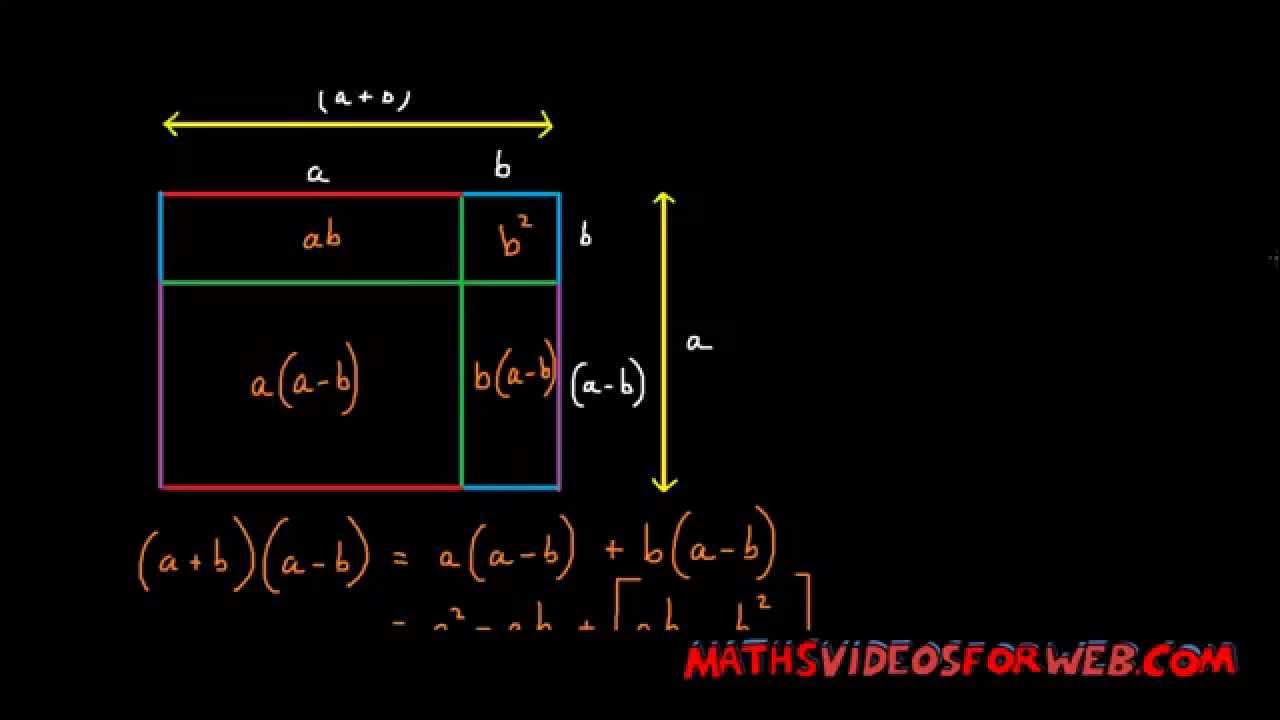


A B A B A 2 B 2 The Real Proof Difference Of Two Squares Demystified Youtube



In A Reaction A B2 Ab2 Identify The Limiting Reagent If Any In The Following Reaction Mixtures I 300 Atoms Of A 0 Molecules Of B2 Ii 2 Mol A
If a/b =2 then what will be 4b/a Look at the equation, a/b=2 so therefore a = 2b Now that we know the value of a, that is, 2b, In this equation, 4b/a, All we have to do is substitute the values of a (2b) since a = 2b, then, 4b/2b By normal division, you'll get 2 as the answerSolution for X (ab2)=100 equation Simplifying X (a b 2) = 100 Reorder the terms X (2 a b) = 100 Remove parenthesis around (2 a b) X 2 a b = 100 Reorder the terms 2 X a b = 100 Solving 2 X a b = 100 Solving for variable 'X'(a−b) 2 = a 2 − 2ab b 2 If you want to see why, then look at how the (a−b) 2 square is equal to the big a 2 square minus the other rectangles (a−b) 2 = a 2 − 2b(a−b) − b 2


Q Tbn And9gcsxj6nch9jkvcgw2jprateqxk Fehjaprpo Txh0pvbjcp 2po Usqp Cau



Example 5 R A B 2 Divides A B Is Equivalence Relation
No, because matrix multiplication is not commutative in general, so (AB)(AB) = A^2ABBAB^2 is not always equal to A^2B^2 Since matrix multiplication is not commutative in general, take any two matrices A, B such that AB != BA11 Evaluate (ab) 2 = a 22abb 2 Step 2 Pulling out like terms 21 Pull out like factors 2ab 2b 2 = 2b • (a b) Equation at the end of step 2 2b • (a b) = 0 Step 3 Theory Roots of a product 31 A product of several terms equals zero When a product of two or more terms equals zero, then at least one of the terms must(a b) 2 This can also be written as = (a b) (a b) Multiply as we do multiplication of two binomials and we get = a(a b) b(a b) = a 2 ab ab b 2 Add like terms and we get = a 2 2ab b 2 Rearrange the terms and we get = a 2 b 2 2ab Hence, in this way we obtain the identity ie (a b) 2 = a 2 b 2 2ab



If A B 11 And Ab 24 Then A 2 B 2



If A 2 B C B 2 C A C 2 A B Are In Ap Then Prove That A B C Are In Ap Mathematics Topperlearning Com Yzhqah
We answer the question whether for any square matrices A and B we have (AB)(AB)=A^2B^2 like numbers We actually give a counter example for the statement$\implies$ $(ab)^2 \,=\, a^2b^22ab$ Simplification The subtraction of two times product of two terms from the sum of the squares of the terms is simplified as the square of difference of the termsSimplify (ab)^2(ab)^2 Simplify each term Tap for more steps Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps



What Is Formula A B Quora



A Well Known Visual To Explain A B 2 2ab B2 A B 2 2ab B2 Math Concepts Math Homeschool Math
And you should be extremely careful not to assume anything about the determinant of a sum Nerdy Sidenote One large vein of current research in linear algebra deals with this question of how detA and detB relate to det(AB)One way to handle the question is this instead of trying to find the value forProbably the answer would be yes and is simple Everybody knows it and when you multiply (ab) with (ab) you will get a plus b whole square (ab) * (ab) = a 2 ab ba b 2 = a 2 2ab b 2 But how did this equation a plus b whole square became generalized Let's prove this formula geometrically( Please refer to the pictures on the side)When you square a binomial, you multiply it by itself (a b)^2 = (a b) (a b) = a (a) a (b) b (a) b (b) {used foil method} = a^2 ab ab b^2 {multiplied through} = a^2 2ab b^2 {combined like terms} (a b)^2 = (a b) (a b) = a (a) a (b) b (a) b (b) {used foil method}


Anti Rabbit Igg H L F Ab 2 Fragment Alexa Fluor 647 Conjugate Cell Signaling Technology


Q Tbn And9gcsoyk0sqjqq745wg2j9ty8pz0ldvzb Uk6 Dmdjulvfglckynuz Usqp Cau
And that can be produced by the difference of squares formula (ab) (a−b) = a 2 − b 2 Like this ("a" is 2x, and "b" is 3) (2x3) (2x−3) = (2x) 2 − (3) 2 = 4x 2 − 9 So the answer is that we can multiply (2x3) and (2x−3) to get 4x2 − 9A and b are the other two sides ;B) b² = a ² 2 a b b ² In woorden Het kwadraat van een verschil is de som van het kwadraat van de eerste term, het tegengestelde van het dubbel van het product van de twee termen en het kwadraat van de tweede term



Boss Ab 2 2 Way Selector Pedal Sweetwater



A B 2 A 2 B 2 2ab Geometrical And Numerical Proof With Calculation
First, multiply each side of the equation by #color(red)(2)# to eliminate the fraction while keeping the equation balanced #color(red)(2) xx A= color(red)(2) xx h/2There is stated that the thesis for the proof is short multiplication formula $$(2)\space\space\space\space\space\space\space\space\space(ab)^2=a^22abb^2$$ Substracting from the short multiplication $(2)$ formula $4ab$ and using square root yields the proof by implicationA 2 b 2 = (ab) (ab) (Difference of squares) a 3 b 3 = (a b) (a 2 ab b 2) (Sum and Difference of Cubes) x 2 (ab)x AB = (x a) (x b) if ax 2 bx c = 0 then x = ( b (b 2 4ac) ) / 2a (Quadratic Formula) Contact us Advertising & Sponsorship Partnership Link to us © 0005 Mathcom


How Does A B 2 Become A B 2 4ab Brainly In



Solved 2 2 Product Formulas Real Numbers A B C Whole N Chegg Com
A 2 b 2 = c 2 Note c is the longest side of the triangle;Square Formulas(a b)2= a2 b2 2ab(a − b)2= a2 b2− 2aba2− b2= (a − b) (a b)(x a) (x b) = x2 (a b) x ab(a b c)2= a2 b2 c2 2ab 2bc 2caA 2 b 2 = (a b) 2 = a 2 2 a b b 2 a^2 b^2 = (ab)^2 = a^2 2ab b^2 a 2 b 2 = (a b) 2 = a 2 2 a b b 2 This is clearly not an identity since 2 a b 2ab 2 a b is not always 0 Thus, we can conclude that this is an identity if and only if 2 a b = 0 2ab = 0 2 a b = 0 Proof 3 Geometric interpretation We can also look at this geometrically and immediately see that it is false


Www Nextgurukul In Questions Answers Forum Question Academic Show That A B 2 B2 And A B 2 Are In Ap



In Any Triangle Abc A B 2sin 2c 2 A B 2cos 2c 2 3biffjff Mathematics Topperlearning Com
Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations (ab)^2(ab)^2 so that you understand betterThere are various student are search formula of (ab)^3 and a^3b^3 Now I am going to explain everything below You can check and revert back if you like you can also check cube formula in algebra formula sheet a2 – b2 = (a – b)(a b) (ab)2 = a2 2ab b2 a2 b2 = (a –For a square b square watch http//youtube/24gWbMSEVVwLearn how a minus b whole square can be explained using geometrical drawingsFor more such videos v



Productos Notables Problemas Resueltos



Boss Ab 2 2 Way Selector
For a square b square watch http//youtube/24gWbMSEVVwLearn how a minus b whole square can be explained using geometrical drawingsFor more such videos vRelated Documents Binomial Theorem Binomial theorem for positive integers;Here is a list of Algebraic formulas – a 2 – b 2 = (a – b) (a b) (a b) 2 = a 2 2ab b 2 a 2 b 2 = (a b) 2 – 2ab (a – b) 2 = a 2 – 2ab b 2 (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca (a – b – c) 2 = a 2 b 2 c 2 – 2ab 2bc – 2ca



Algebra Sleuth Proof That 1 2 Activity Education Com
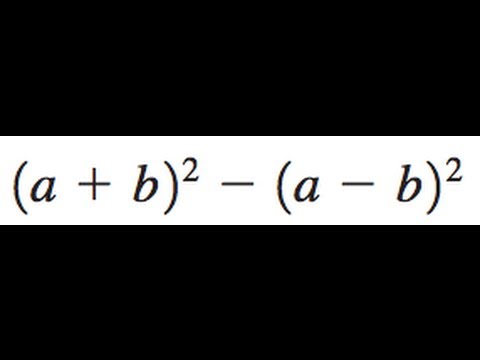


Factor A B 2 A B 2 Youtube
Holds only in fields of characteristic 2, which if finite, must have 2^m elements, where m is a positive integer Also holds in the (infinite) field of rational functions over such a field


If A B Ab 4 1 Then What Is A B Quora


If A B 3 And B2 29 Find The Value Of Ab Quora


Q Tbn And9gcrswdldblxmiitn Ggstx6knbcgxw3sex0r673zeswoh Igfkvn Usqp Cau
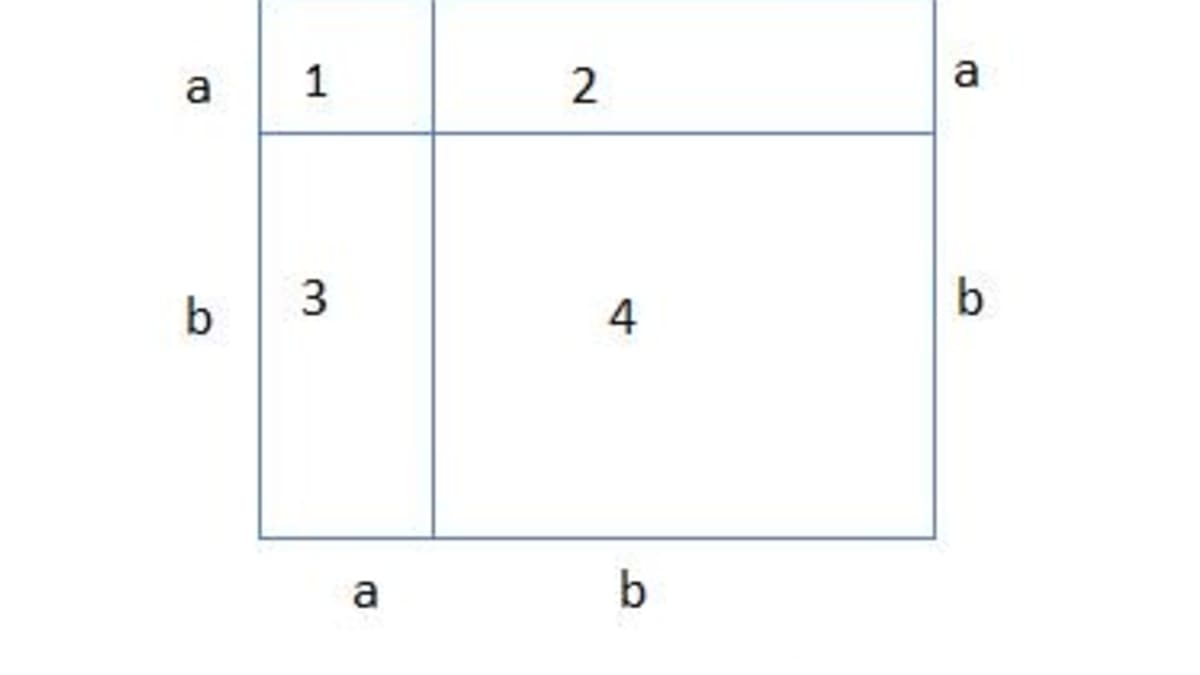


Why A B 2 B2 2ab Owlcation Education



A 2 B 2 A B 2 C 2 D 2 C D 2 A B C D Are Positive Integers Fun With Num3ers



Show That If 2 A 2 B 2 A B 2 Then A B



If A 2 1 3 B 2 3 4 C 1 2 7 Are Three Points Find A Point D Such That Ab 1 2 Cd Math Vector Algebra Meritnation Com



If A B C X 2 B C A Xy C A B Y 2 Is A Perfect Square Then A B C Are In A Ap B Gp C Hp D Not Of The Above


In How Many Ways Can You Write The Formula A B 2 Quora



Special Binomial Products



Manipulating Expressions Using Structure Example 2 Video Khan Academy
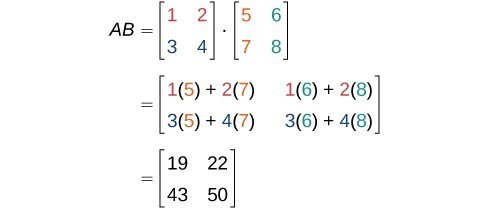


Finding The Product Of Two Matrices College Algebra



16 A B 2 9 A B 2 Factorise Brainly In



Ex 1 4 2 Determine Whether Is Commutative Class 12 Ncert



Factorise B2 2 Ab Ac Brainly In



Prove That Axxb 2 A 2b 2 A B 2 Youtube
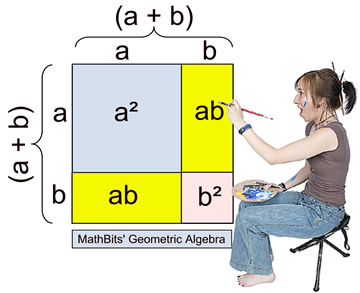


Special Binomial Patterns Mathbitsnotebook A1 Ccss Math
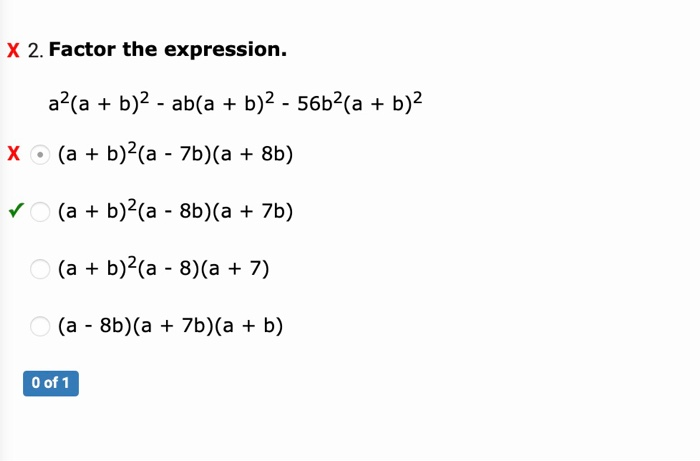


Solved X 2 Factor The Expression A B 2 Ab A B 2 Chegg Com



Solved 1 Let A And B Be Sets Prove That A B U B Chegg Com



If A 2 B 2 4 And Ab 2 What Are A 2 B 2 Quora



A B 3 Y Ab 1 Halla B2 Youtube



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo
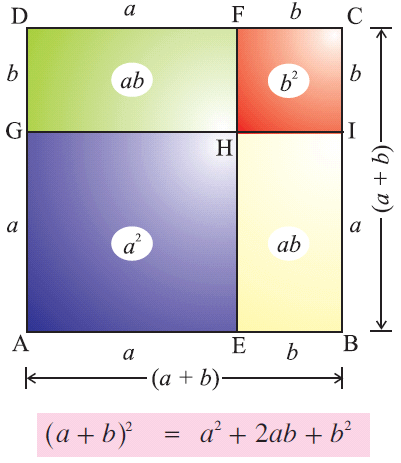


Formula For A Plus B Whole Square



Icsepapers If A 2 B 2 29 And Ab 10 Find A B



Binomial Theorem Formula



Solved Establish The Formula Ab A B 2 2 A B 2 2 Chegg Com
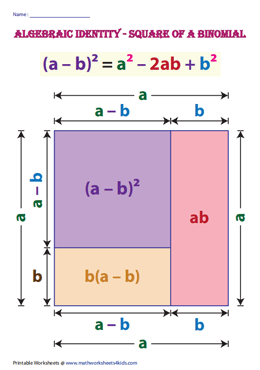


Algebraic Identities Charts Printable Formulas
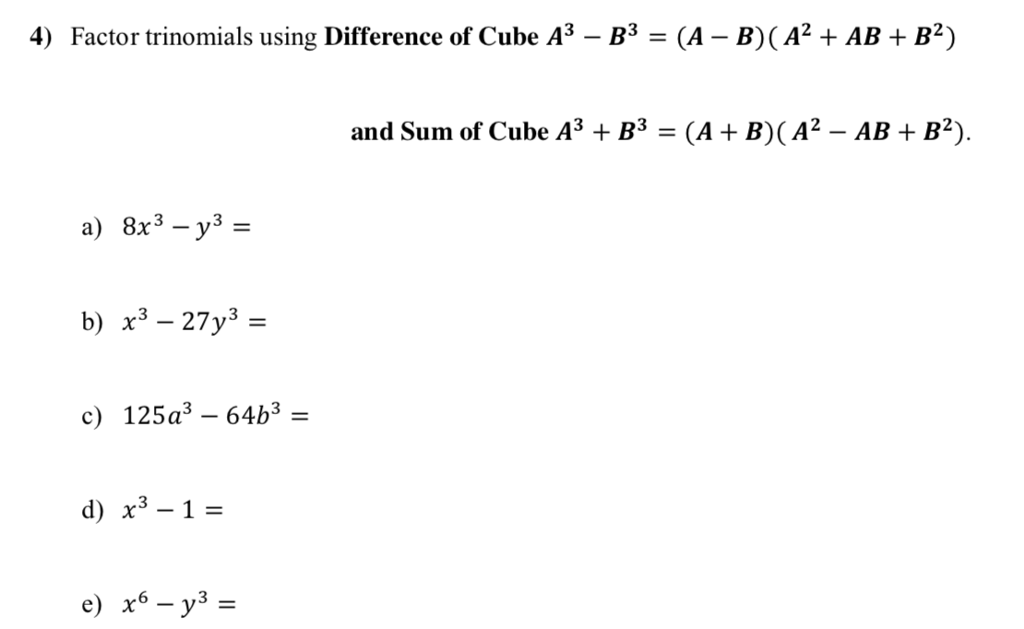


Solved 3 Factor Trinomials Using Perfect Square Formula Chegg Com


Difference Of Cubes Math Central



The Binomial Theorem A B 2 A B A B 2ab B2 Ppt Video Online Download



Prove A Group Is Abelian If Ab 2 A 2b 2 Problems In Mathematics
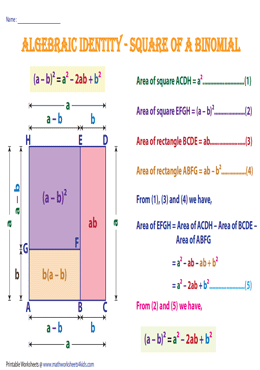


Algebraic Identities Charts Printable Formulas



How To Expand Using The Identity A B C 2 B2 C2 2ab 2bc 2ca Youtube



If A 1 2 3 4 2 5 And B 2 4 23 5 1 Then Find Ab Ba Show T



Ex 12 3 4 If A 2 B 2 Find Value Of I A 2 B 2


If Math A B 3 Math And Math A 2 B 2 7 Math What Is Math A 4 B 4 Math Quora


If A B 11 And B2 65 What Is A3 Quora


Http Thewe Net Math Gelfand Gelfand3 Pdf



Math Labs With Activity Verify The Identity A B A 2ab B A Plus Topper
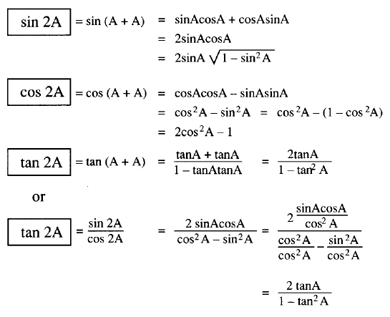


Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab



Factorizacion Y Productos Notables 2 A B C


A Short Course In Math


Http Thewe Net Math Gelfand Gelfand3 Pdf


Show That A B 2 A 2 B 2 And A 2 B 2 Are In Ap Sarthaks Econnect Largest Online Education Community


Algebra Formula Bank Open Algebra Formula Bank



If A B 5 And Ab 2 Find A B 2 Brainly In


Identites Remarquables De Degre Superieur A 2



How To Factorise Using The Identity A B 2 B2 2ab Youtube



Solved 10 Answer The Following You Do Not Need To Show Y Chegg Com



How To Expand Using The Identity A B 2 B2 2ab Youtube



Ex 12 3 10 Simplify Expression And Find Its Value If A 5 B 3


How Is A B A 2ab B Can You Explain Quora



A B 2 A B 2 4ab Brainly In



Ex 1 1 16 Let R A B A B 2 B 6 Choose Ex 1 1
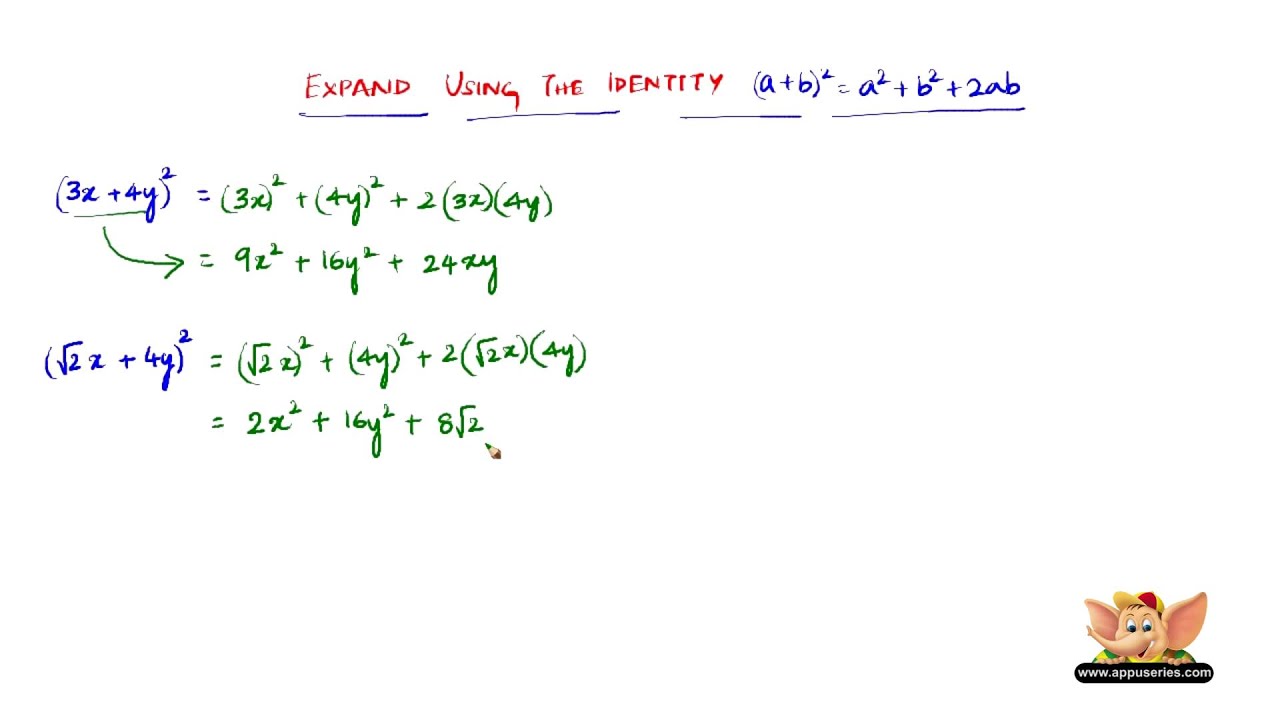


How To Expand Using The Identity A B 2 B2 2ab Youtube



How To Factorise Using The Identity A B 2 B2 2ab Youtube



If B2 9 And Ab 4 Find The Value Of 3 A B 2 2 A B 2 Brainly In
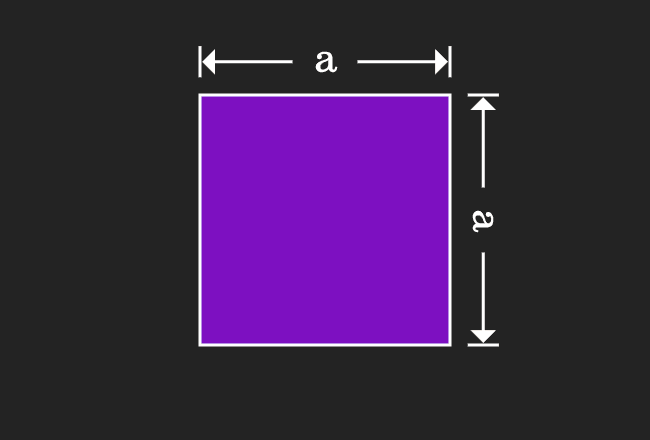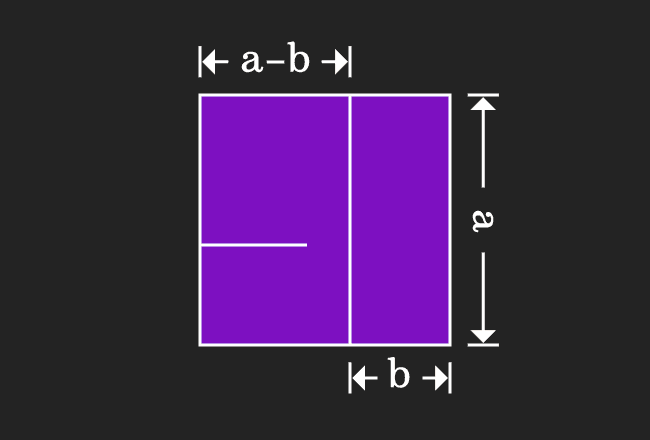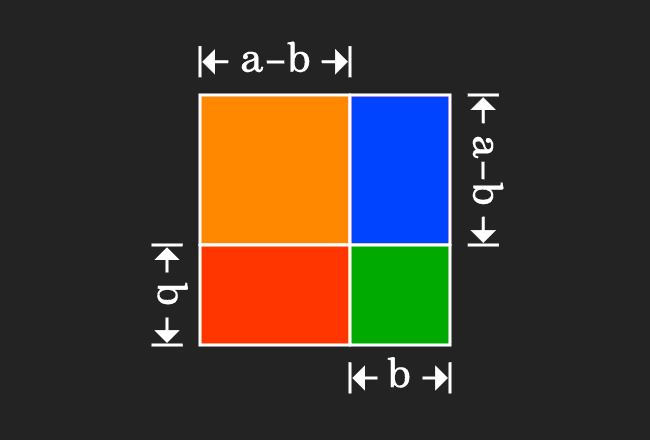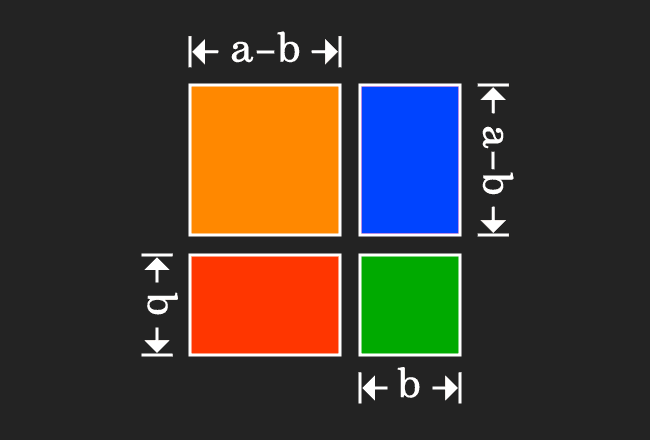


Proof Of A B Formula In Geometric Method



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo


Derivation Of Formula For A B 3


How To Prove That 2cos A B 2 Cos A B 2 2sin B A 2 Sin A B 2 Sin A B Sin A B Quora


Derivation Of Formula For A B 2



A B 2 5 B2 24 A B 2 Factorize Brainly In



Ex 14 4 13 Find And Correct 2a 3b A B 2a 2 3b 2


Math Eloquently A Plus B Squared



If A And B Are Square Matrices Of The Same Order Then A B 2 A 2 2ab B 2 Implies A Ab 0 Youtube
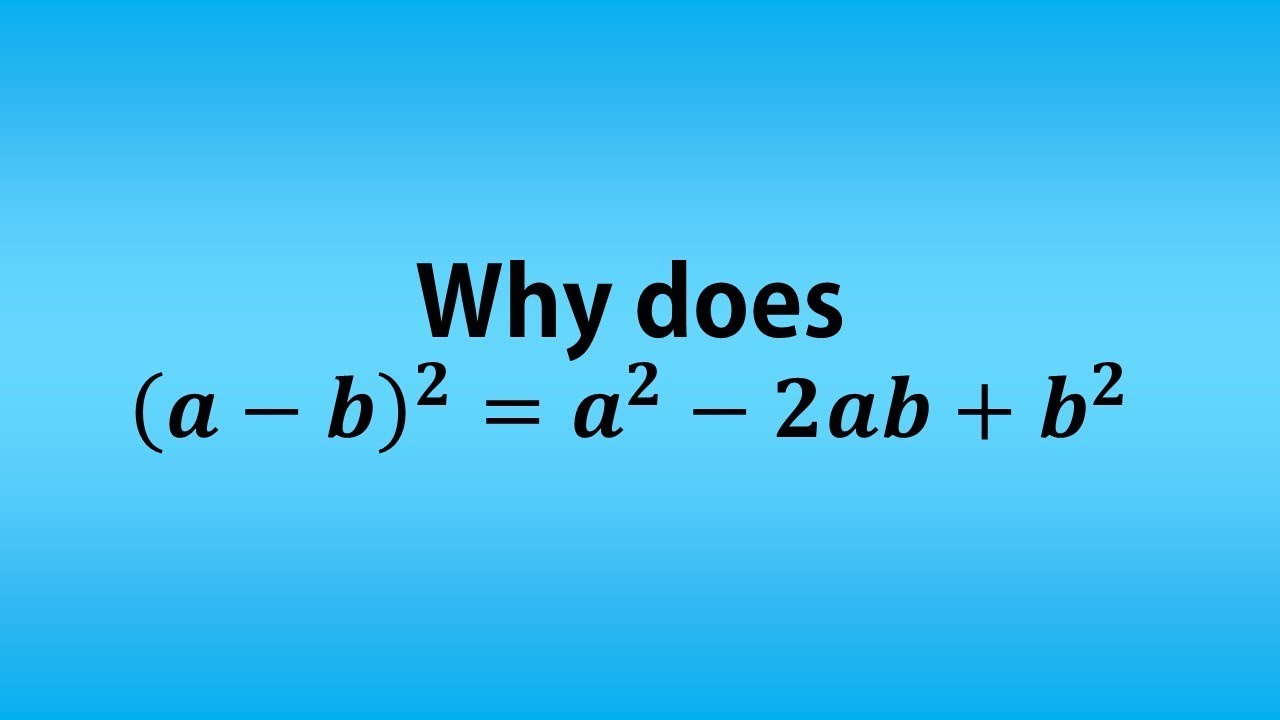


Why Does A B 2 A 2 2ab B 2 Youtube


If B2 C2 Ab Ca 0 Prove That A B C Polynomials Maths Class 9



Solved X 2 2 X 2 X 2 Which Of The Following Is Chegg Com



A B Formula Identity



A B 2 Formula Learn Formula For Calculating A B 2 Cuemath
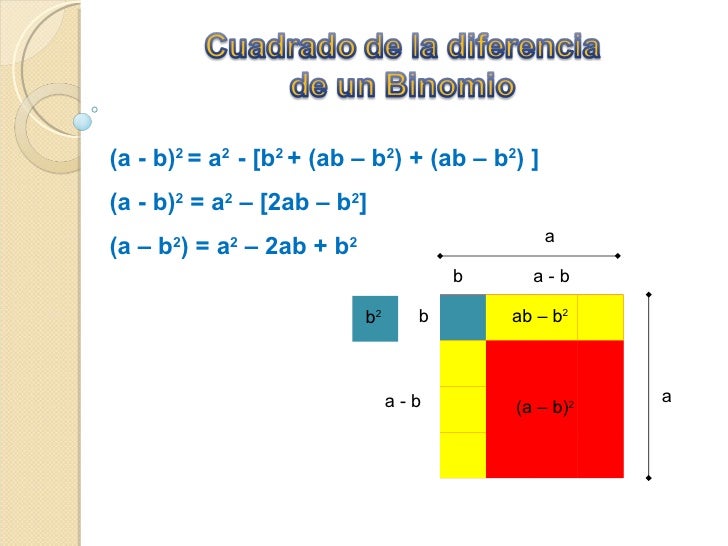


Productos Notables Graficos



Cos A B Sin A B 2 Sin 45 0 A Cos 45 0 B Youtube



Formula Of Ab 3 Is Please Answer This Brainly In


コメント
コメントを投稿